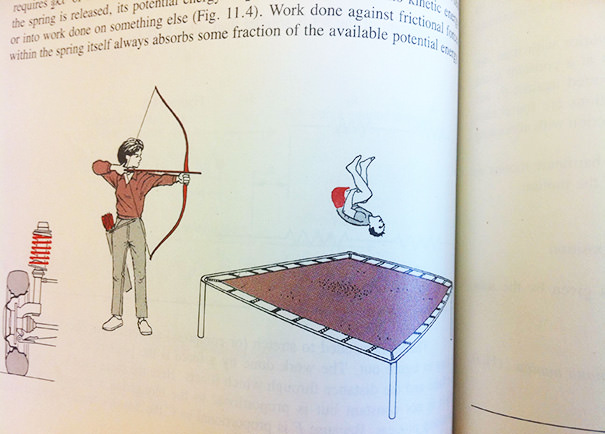
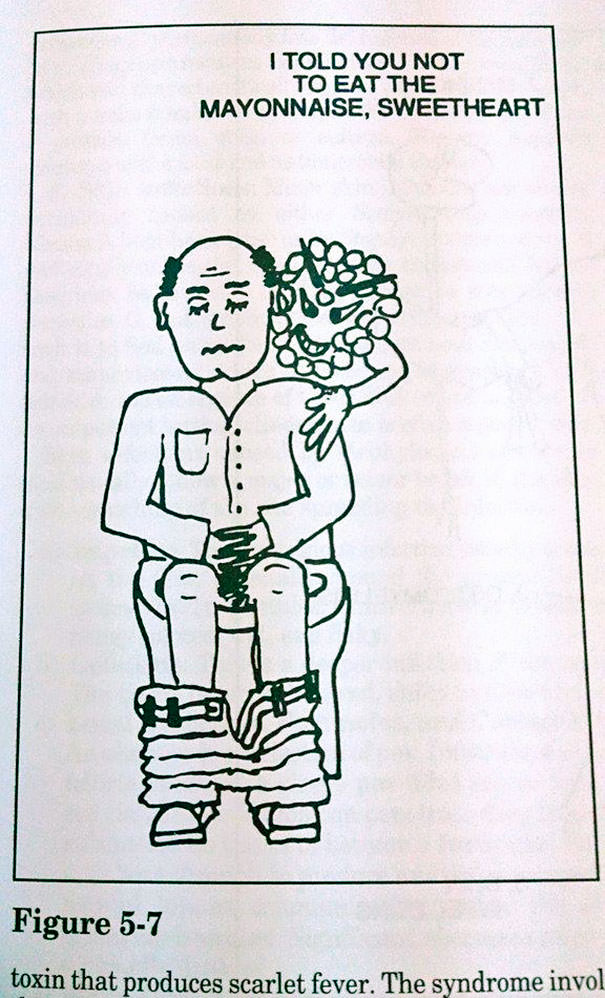
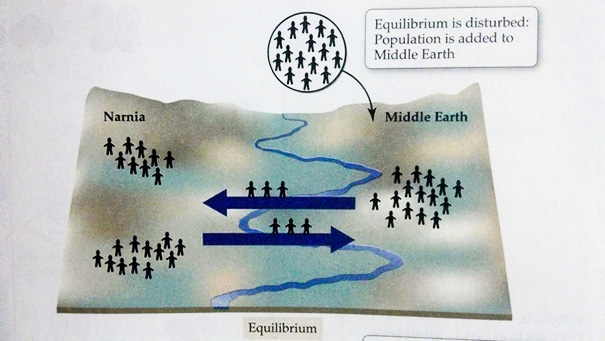
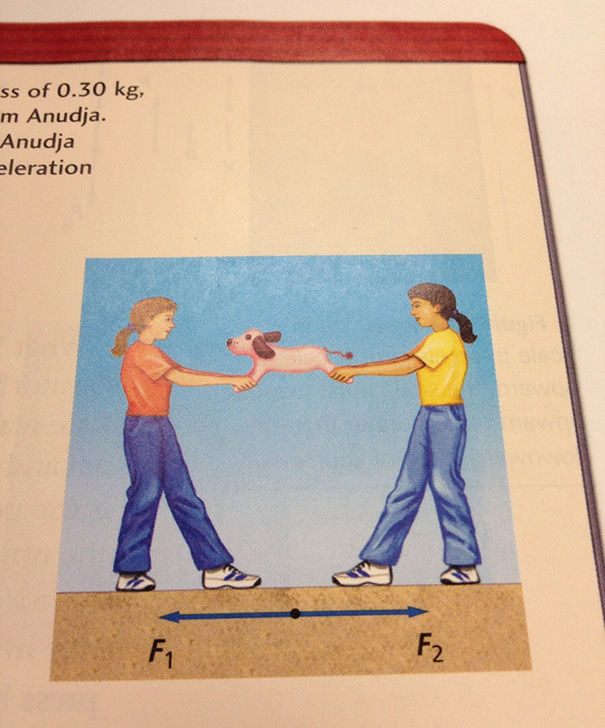
Textbooks are the most boring thing for a student. All those facts, all those graphs and all those diagrams are dense and utterly boring. Textbooks are actually written by real human, but they seem like they’re written by robots. However, the authors of books listed below tried to inject a modicum of humor into dry textbooks. Some of them appear to be officially approved. Others appear to be subtly hidden where nobody will find them, but all of them are guaranteed to make you laugh.